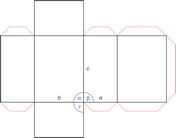
RELACION DE LOS POLIEDROS CON LAS ESTRUCTURAS CRISTALOGRÁFICAS
SISTEMAS CRISTALINOS Y REDES DE BRAVAIS
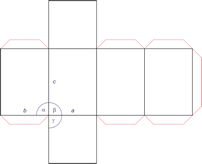
Un sólido cristalino se construye a partir de la repetición en el espacio de una estructura elemental paralelepipédica denominada celda unitaria. En función de los parámetros de red, es decir, de las longitudes de los lados o ejes del paralelepípedo elemental y de los ángulos que forman, se distinguen siete sistemas cristalinos y se dividen en: cúbico, hexagonal, tetragonal, trigonal, rómbico, monoclínico y triclínico.
Una red de Bravais (físico francés A. Bravais ) es un arreglo infinito de puntos discretos con un ordenamiento y orientación, que parece exactamente la misma, desde cualquier punto de observación. En 1848 el físico e mineralogista francés Auguste Bravais (1811-1863) descubrió que sólo hay 14 redes únicas en los sistemas cristalinos tridimensionales.
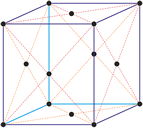
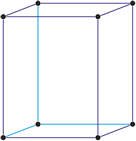
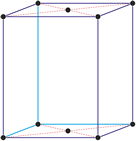
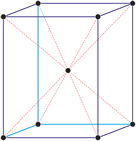
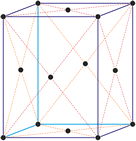
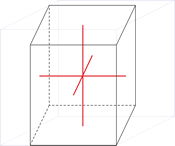
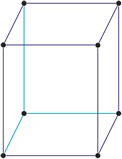
Sistema cristalino cúbico
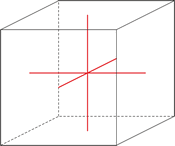
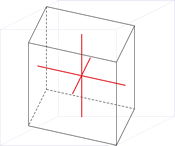
Ejes cristalográficos
Modelo 3D
En el sistema cúbico (ó isométrico) los tres ejes cristalográficos son todos de igual longitud y cortan a los ángulos rectos (90°).
a = b = c
α = β = γ = 90°
Volumen de la celda unitaria
V = a3
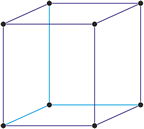
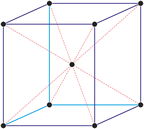
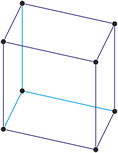
Redes de Bravais
primitiva (cP)
centrada en el cuerpo (cI)
centrada en las caras (cF)
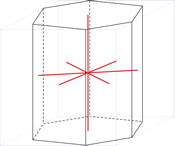
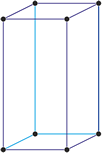
Sistema cristalino hexagonal
Ejes cristalográficos
Modelo 3D
El sistema hexagonal se caracterizan por tener cuatro ejes. Tres ejes (denotado por a1, a2 y a3) de igual longitud se encuentran en un plano y se cruzan en un ángulo de 120° (entre los extremos positivos). El cuarto eje (c) es más largo o corto que los otros tres y forma con ellos ángulos rectos.
Celda unitaria hexagonal
Los parámetros parámetros de la celda unitaria son:
a = b ≠ c
α = β = 90° γ = 120°
El volumen de una celda unitaria hexagonal es
V = a2c sin(60°)
Red de Bravais
primitiva (hP)
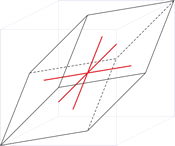
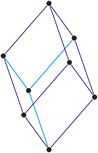
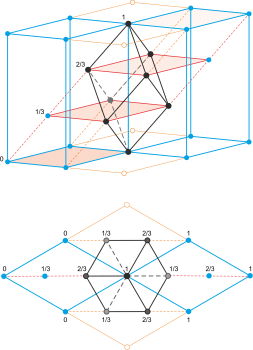
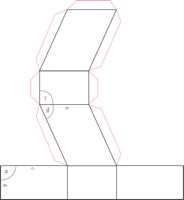
Sistema cristalino trigonal
Ejes cristalográficos
Modelo 3D
Los ángulos entre los ejes del cristal, en el sistema trigonal o rombohédrico, son idénticos, pero diferentes de 90°, y las tres dimensiones del cristal unitario son idénticas. El sistema de ejes romboedrales es de dificil uso, y generalmente se suele evadir utilizarlo. En su lugar, se prefiere disponer de un sistema de ejes hexagonales.
a = b = c
α = β = γ ≠ 90°
A la hora de describir la estructura de un sólido cristalino con simetría rombóedrica los cristalógrafos prefieren a menudo describir la estructura con una celda unitaria hexagonal no primitiva.
a = b ≠ c
α = γ = 90° β = 120°
Volumen de la celda unitaria
Referido a los ejes romboédricos
V = a3 (1 - cosα) √1 + 2cosα
Referido a los ejes hexagonales
V = a2c sin(60°)
Redes de Bravais
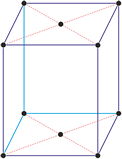
celda romboédrica primitiva (hR)
celda hexagonal R-centrada (hR)
La figura muestra la relación existente entre la celda romboédrica primitiva y un celda hexagonal
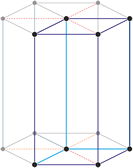
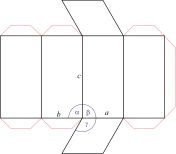
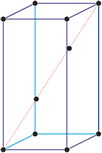
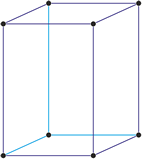
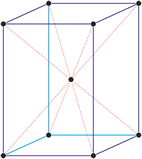
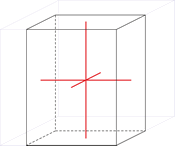
Sistema cristalino tetragonal
Ejes cristalográficos
Modelo 3D
En el sistema tetragonal dos ejes son iguales y uno diferente (más corto o más largo) pero todos ellos son perpendiculares entre sí.
a = b ≠ c
α = β = γ = 90°
Volumen de la celda unitaria
V = a2c
Redes de Bravais
primitiva (tP)
centrada en el cuerpo (tI)
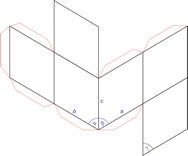
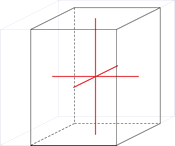
Sistema cristalino rómbico
Ejes cristalográficos
Modelo 3D
En el sistema rómbico (o ortorrómbico) los ejes de referencia son desiguales y perpendiculares entre sí.
a ≠ b ≠ c
α = β = γ = 90°
Volumen de la celda unitaria
V = abc
Redes de Bravais
primitiva (oP)
centrada en las bases (oC)
centrada en el cuerpo (oI)
centrada en las caras (oF)
Sistema cristalino monoclínico
Ejes cristalográficos
Modelo 3D
En el sistema monoclínico dos de tres ejes de referencia desiguales se cortan oblicuamente (no de 90°) y el tercero es perpendicular al plano de los otros dos.
a ≠ b ≠ c
α = γ = 90° ≠ β
Volumen de la celda unitaria
V = abc sinβ
Redes de Bravais
primitiva (mP)
centrada en las bases (mC)
Sistema cristalino triclínico
Ejes cristalográficos
Modelo 3D
En el sistema triclínico los tres ejes cristalográficos son todos desiguales en la longitud y se cortan a tres ángulos diferentes (cualquier ángulo pero diferentes de 90°).
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
Volumen de la celda unitaria
V = abc √1 - cos2α - cos2β - cos2γ + 2cosα·cosβ·cosγ
Red de Bravais
primitiva (aP)